Filter Slope

The slope of a low-pass filter refers to how much attenuation you get as you go up one octave on the frequency scale. Usually, synthesizers have two filter slopes available: 12 db and 24 db. If we look at a 12 db low-pass filter and a given (harmonic) frequency past the cutoff, the frequency one octave higher is attenuated by 12 db. Same idea for the 24 db filter. The 24 db filter has more slope than the 12 db filter and the harmonic frequencies are attenuated faster.

The question is: what kind of filter slope does the Korg DS-10 Voltage Controlled Filter (VCF) has exactly?

Let's find out! Let's crank the resonance (peak) all the way up and tune our (now resonant) cutoff frequency to A4 (440 Hz) playing A4s with a saw-tooth waveform on oscillator 1. You may want to use an audio editing software (say cool edit pro but audacity would do as well) to tune the cutoff frequency if you don't have good ears (like me). Once the filter cutoff frequency is set to A4, we can turn the peak all the way down so that we only hear the filtered signal. Now, we need to do an harmonic analysis of the filtered signal using your favorite audio editing software.


Well, here it is! The 1st peak is the fundamental (A4 at 440 Hz) and the other peaks are the harmonics. We are gonna look at the attenuation between the 2nd peak (861 Hz) and the 4th peak (1765 Hz). Those two harmonics, about one octave apart, are past the cutoff frequency (440 Hz) and are therefore attenuated according (hopefully) to the slope of the filter. The level of the 2nd peak is about -36 db while the level of the 4th peak is about -54 db, a drop of 18 db. This would mean that the slope of the filter is...18 db. Not quite! We are missing a little bit of something: the 4th peak is weaker than the 2nd even without filtering so we have to take that into account.


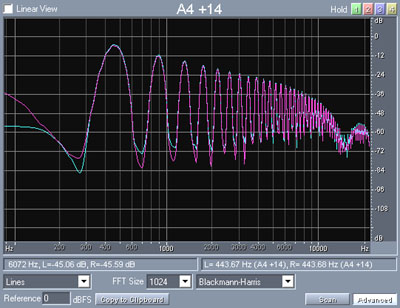
Without any filtering (what is shown just above), the 4th peak is 6 db below the 2nd peak, so the filter slope is actually 12 db (18 db minus 6 db).

Hopefully, somebody else will be able to confirm or infirm this. Maybe, this methodology is flawed and there's a better (and most importantly right) way to figure this out? In all cases, I'd like to know.

Next, it would be a good idea to calibrate the filter cutoff, that is, know the actual cutoff frequencies for evenly spaced knob positions.

Why all this? Because it will enable us to borrow patch settings from other synthesizers and apply them to the Korg DS-10. Hopefully.